Geometry in Harmony

They say you can’t dance about architecture.  But can you hear geometry?  I sure think so.  Below are a few examples of "shapes" in jazz music.  The examples below show that John Coltrane heavily explored this concept, but there were some earlier practitioners too.  The examples below are all transposed to the key of C.

The Regular Polygons 

Equilateral Triangle: The song "Giant Steps" is based around Coltrane Changes, which rotates around three key centers.  The interval between each of the three key centers spans a major third, which builds an augmented triad.  If you connect the tonalities in the circle of fifths you get an equilateral triangle.  The name "Giant Steps" may come from the fact that the intervals between the three key centers are much larger than the ears are used to hearing in music.  This harmony is used in other Coltrane songs, like "Countdown," Coltrane's reharm of "But Not For Me," and the bridge of "Have You Met Miss Jones."  

Perfect Square:  This progression is based off minor third rather than the major third intervals, forming a perfect square.  You can find this progression in Coltrane's "Central Park West," which alternates around four tonal centers: BM7-DM7/AbM7-FM7 (transposed to the key of C in the figure below).  

You can substitute this progression for any standard turnaround, CM7-A7/Dm7-G7/CM7.  Why?  In both progressions you start and end on a CM7.  Sure, the chords in-between aren't related to each other, but that doesn't really matter.  The reharm gives the turnaround  a cool "outside" sound before finally resolving to the right place at the right time.  You can also try playing it backwards...

Dodecagon: One improvisation technique jazz players commonly use is called "back cycling," or working backwards from your target landing (ending) chord and substituting a series of ii-Vs through the Circle of 5ths for as far back as you’d like.  

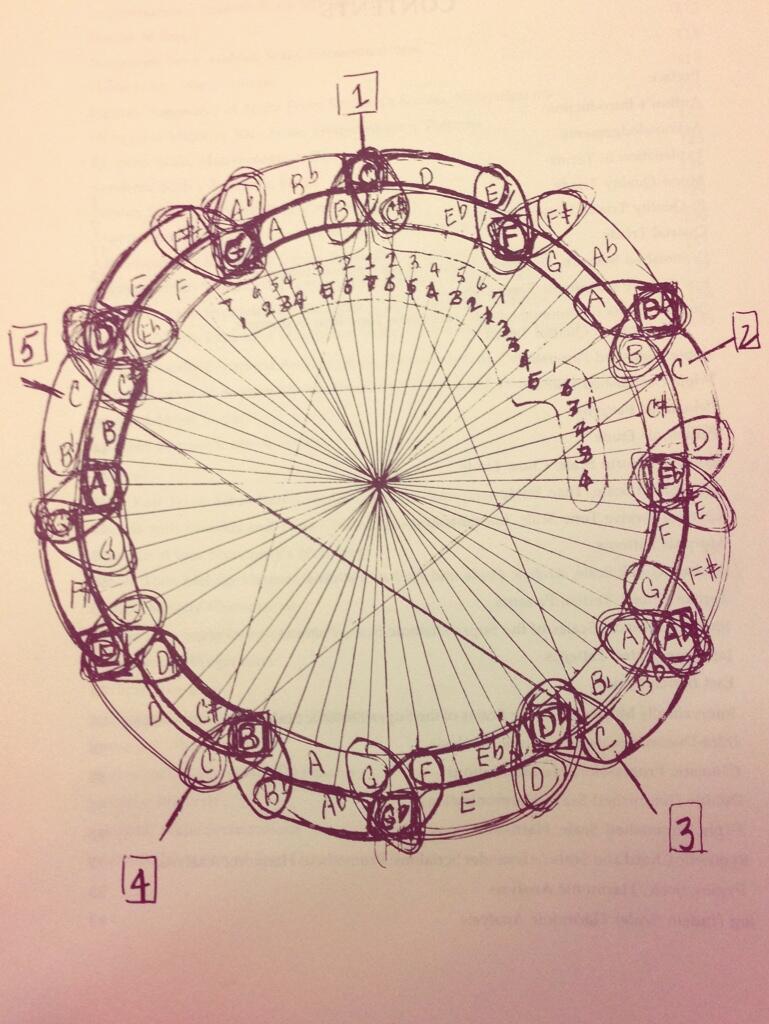
While there are many examples to choose from, one of my favorite recordings of this concept is played by Don Byas over Rhythm Changes.  The back cycling may sound outside for a bit at the start, but as soon as you reach your target landing chord it all seems to come together and make sense. Why does this work?  If you're a physicist you can describe it as "harmonic gravity" that pulls you to your landing chord.  If you're a geometrician, you would trace out the harmonic movement over the Circle of 5ths, as shown below.

Sure this is not a regular polygon, or any polygon at all.  But you'll notice the equidistant intervallic movement, and that if the back cycling was continued longer then the form would eventually create dodecahedron.  So even though Don Byas is not playing a full dodecahedron, he is implying it.  

*note: the more sides you add to a regular polygon, the closer you get to a circle.  In Western music the closest you can get to playing a circle is a dodecahedron as there are only 12 tones in the scale.  If you play more Eastern music or get into "microtones" you could play a circle.  I wonder what that sounds like!

Other Shapes  

For reference, here are other shapes that are created by other common chord progressions.

Blues:

Turnaround:

Smells Like Teen Spirit: This example is one I found from Ethan Hein's blog.  (http://www.ethanhein.com/wp/2016/musical-simples-smells-like-teen-spirit/)

While these chord progressions sound great, they are not regular polygons and cover a pretty minimal amount of the Circle of 5ths.  Thus, they do not have the the distinctive sound and expansive harmony so often used by Coltrane and others.

Thoughts to leave you with: playing a pentagram
Now if I could only understand the Coltrane Pentagram...it still eludes me...